¿Cómo calcular la desviación típica en una hoja de cálculo de Microsoft Excel? Guía paso a paso

Cuando se trabaja en programas de hojas de cálculo se deben utilizar constantemente fórmulas y ecuaciones matemáticas para llevar a cabo diferentes tipos de operaciones matemáticas. En este aspecto Excel cuenta con una gran cantidad de ventajas ya que su repertorio de funciones es muy amplio.

Es así como aquí también vas a tener la oportunidad de calcular lo que es la desviación típica, la cual se trata de una medida de dispersión que indica en un conjunto de datos cuanto pueden alejarse los valores con respecto a la media o promedio. Lo que hace que se convierta en una función más que necesaria al momento de conocer cualquier tipo de estadística en los datos que estés manejando.

De esta manera, poder conocer cómo aplicar esta herramienta dentro de la hoja de cálculo de Excel es muy importante, ya que de esa manera podrás conocer las probabilidades de que un evento ocurra o no. Para ello sigue detalladamente todo lo que se te explicará a continuación en el post.

¿Qué es la desviación estándar en estadística y que nos permite conocer?

La desviación estándar o típica como también se conoce es una medida estadística que te permite conocer la información sobre la dispersión media de una variable, por lo que resulta muy interesante cuando se quiere saber cuánto se alejan los valores del valor promedio. Es importante resaltar que la desviación estándar es siempre mayor o igual a cero.

Para que se pueda entender este concepto claramente va a hacer necesario analizar dos conceptos sobre la desviación como lo son los siguientes:

• Desviación: Es la separación que existe entre un valor cualquiera de la serie y la media o promedio como también se le llama.
• Esperanza matemática, media o valor esperado: Esta es la media de la serie de datos de la muestra.

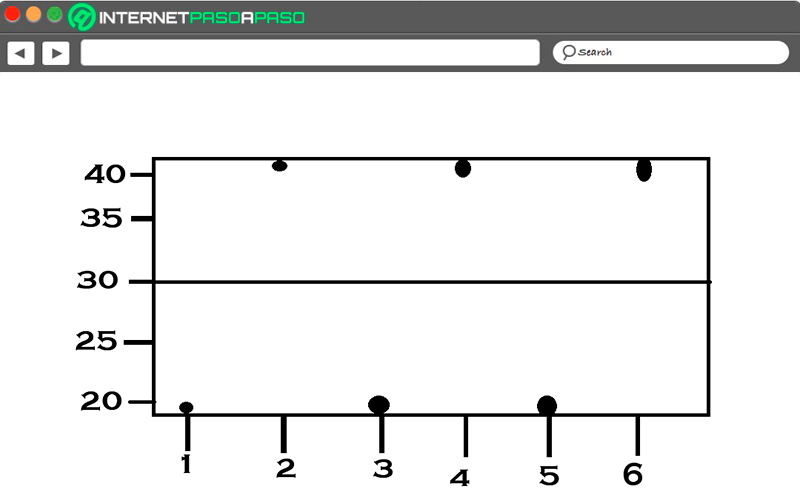
Conociendo estos dos términos, entonces se puede decir que la desviación típica se va a calcular de forma similar a la media, pero en esta ocasión se toman son los valores de la desviación. Aunque este razonamiento es lógico e intuitivo, se tiene un fallo que se puede comprobar con la siguiente imagen.

Como se puede ver, en dicha imagen presentada se observan 6  valores,  esto quiere decir que N=6, la media de las observaciones se encuentra presentada por la línea negra que está situado en todo el centro del gráfico, la misma tiene un valor de 3. Por lo tanto, conociendo la media se puede entender por desviación la diferencia que existe entre cualquiera de las observaciones y la línea negra.

Esto quiere decir que se tiene 6 observaciones por lo que se debe realizar el siguiente procedimiento con cada una de ellas:

• Desviación à (2-3) = -1
• Desviación à (4-3) = 1
• Desviación à (2-3) = 1
• Desviación à (4-3) = 1
• Desviación à (2-3) = -1
• Desviación à (4-3) = 1

Si se puede ver cuando sumas las dos desviaciones, 6 desviaciones y dividimos entre N = 6, el resultado termina siendo cero. La lógica sería que la desviación media fuera de 1, pero una característica matemática de la media con respeto a los valores que la forman es, que la suma de las desviaciones es cero, para poder solucionar esto será necesario elevar al cuadrado las desviaciones.

Pasos para calcular la desviación típica estadística en una hoja de cálculo de Microsoft Excel

Para poder llevar a cabo este cálculo matemático en tu hoja de trabajo de Excel será necesario que realices cada uno de los pasos que te vamos a indicar a continuación:

• Lo primero será ingresar a Microsoft Excel donde tienes los datos con los que estás trabajando o ingresa a un documento en blanco de la aplicación.
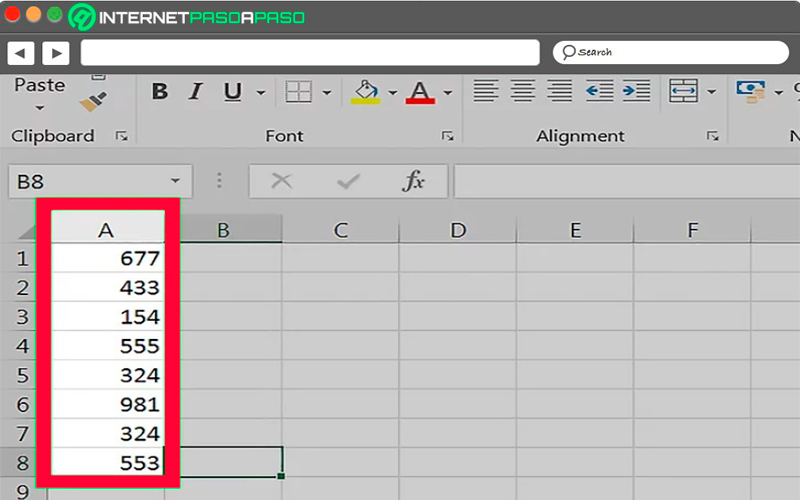
• Lo siguiente será ingresar los valores que quieras utilizar, para ello escoge la columna que quieres y añade cada uno de los datos y seguidamente escribe el valor para cada dato en las celdas. Un ejemplo de esto sería que en la columna A como el área que se ingresan los datos, podrías escribir un número en la celda A1, en la celda A2, en la Celda A3 y así sucesivamente.

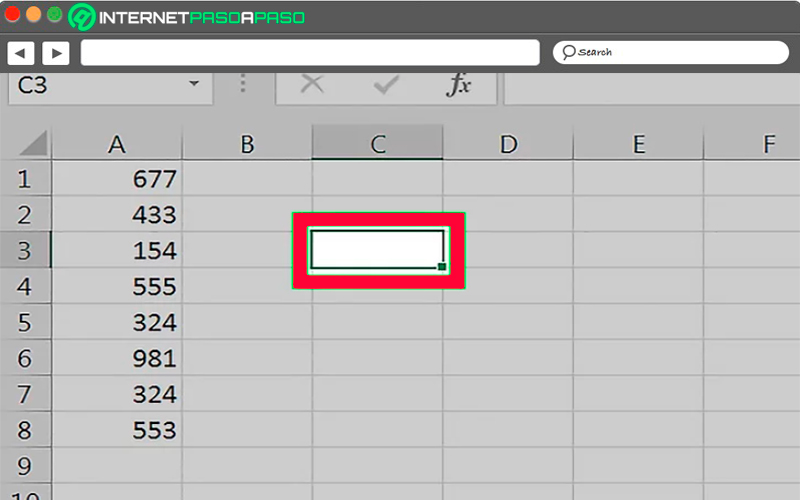
• Una vez hayas ingresado todos los datos en la columna A, lo siguiente será hacer click en una celda en blanco, aquí debes seleccionar la celda donde quieres que se muestre el valor de la desviación estándar.

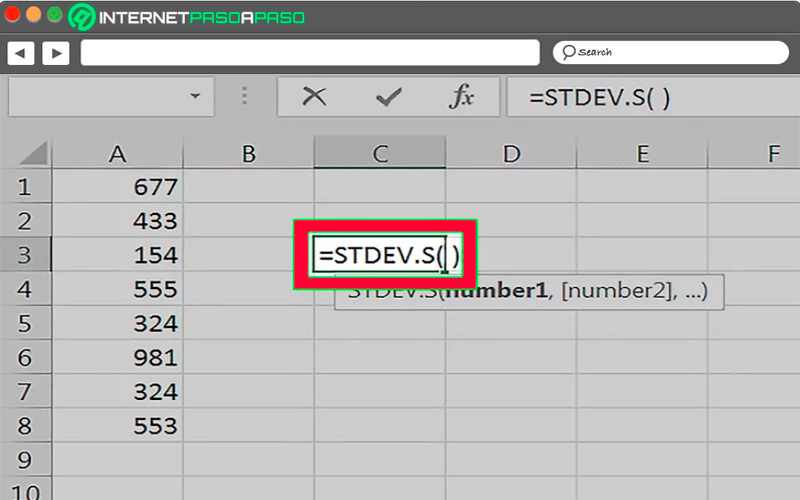
• Lo siguiente será escribir la fórmula de la desviación estándar en la celda vacía que has seleccionado, esta fórmula es la siguiente: =DESVEST.P () donde P significa la “Población”. La desviación estándar de la población toma en cuenta todos los puntos por lo que este será el valor de N.
• Para poder hallar la desviación estándar de una muestra debes escribir la siguiente fórmula =DESVEST.M(). En este caso la desviación estándar de una muestra va tomar en cuenta un valor menos que el número de puntos de datos que tengas (N-1).

• Ahora debes añadir lo que es el rango de valores, entre los paréntesis debes escribir la letra y el número de la celda que contenga la primera porción de datos, escribe dos puntos (:) y seguidamente la letra y el número de la última celda de datos. Esto te permitirá definir el rango a evaluar. Por ejemplo, si estás en la columna A entonces debe colocar desde A1:A10 siendo estas las celdas que contienen todos los datos a evaluar. En el caso que quieras mostrar la desviación típica de valores de distintas celdas entonces será necesario que lo coloques de la siguiente manera: =DESVEST.P(A1,B3,C5).
• Una vez introducido estos datos, debes presionar la tecla “Enter” para que se efectúe la solución de la fórmula y así puedas conocer el resultado de la desviación estándar de la serie de datos que estás evaluando.